如同测量关联度一样，具体采用哪种方法测量影响也取决于变量的类型，具体的请参考“专栏15-2"。影响的测量分成两类：对称（影响）与非对称（影响）。对称影响指两变量间相互影响，并不存在着唯一的影响关系；非对称影响则是指两变量间存在着唯一的影响方向，也就是说存在着自变量和因变量，本章我们只讨论非对称影响关系。

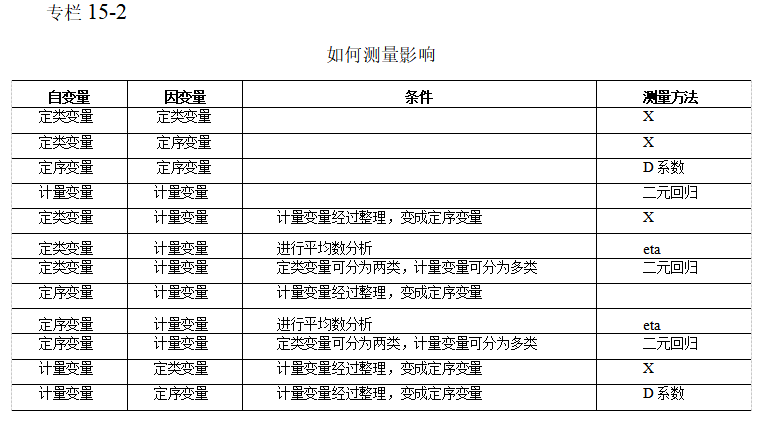
1.Goodman和Krushal'sk

进行双变量探索性分析时，当一个变量为自变量而另一个变量是因变量时，入值用来预测因变量由于自变量变化而变化的程度。入值越大，则一个变量对另一个变量的影响程度越大。

2.D系数

D系数(Somer'sd)描述的是一个定序变量对另一个定序变量的影响程度，D系数的作用和gamma系数相同。D系数本身带有正负号，它能显示出两变量间影响关系的本质。

3.二元回归

二元回归也被称为线性回归(linearregression)或普通最小二乘法(ordinaryleastsquares,OLS)回归。二元回归要求的是两个变量均为可计量变量，二元线性回归是基于两个变量间存在的是线性关系，也就是一个变量的增加会引起另一个变量相应地增加或减少，且两变量间的增加或减少幅度呈一定比例。例如，如果对收入和幸福感两个变量进行线性回归分析时，给定一个人的幸福感，我们就可以计算出其相应的收入水平(见图15-1)。

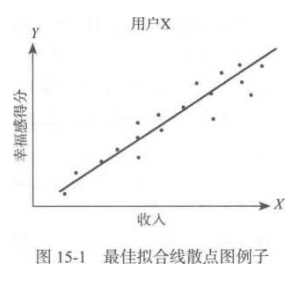
二元回归是指在以自变量为X轴，以因变量为y轴的散点图中，可以沿着各离散点画出一条直线。通过这条回归直线可以看出一个变量对另一个变量的影响程度。二元回归的代数表达式为广=3x+a，其中，x是自变量，y是因变量，8是回归直线的斜率，a是回归直线在纵轴上的截距。可以由相关系数计算而得）。把》标准化，我们可以得到回归系数们双变量的标准相关系数会告诉我们自变量在多大程度上影响因变量。

接下来就是计算回归直线在多大程度上能解释两个变量间的回归关系，因为对不同的变量而言，可能取得相同的回归直线。我们把回归系数R进行平方后得身,这也就是我们之前所讲过的可决系数，R2可以衡量在多大程度上因变量变化是由自变量引起的。

那么，给定自变量的值，回归直线多大程度上解释了因变量的值？也就是对于那些没有落在回归直线上的各个散点，如何进行解释？我们知道，理想情况下，各个散点都应该落在回归直线上，因此对于给定的自变量值，我们先计算其对应的回归值，然后与它的实际因变量值相减，这也就是给定自变量的条件下回归值的误差（error）,也被称为残差（residual）。我们对各个散点做同样的处理，把残差平方然后加总，就得到了估计值的标准差。估计值的标准差和标准差的作用相同，都是用来衡量变量的分布情况：估计值的标准差越大，变量分布越广泛；估计值的标准差越小，则分布越集中。